

1、函数的概念:
在某一个变化过程中,有两个变量x和y,设变量x的取值范围为数集D,如果对于D内的每一个x值,按照某个对应法则f(一个自变量对应一个函数值),y都有唯一确定的值与它对应。那么,把y叫做x的函数,记作y=f(x),数集D叫做函数的定义域。
2、函数的三要素:
(1)定义域:函数的定义域是自变量的取值范围。(函数的定义域就是使得这个函数关系式有意义的实数的全体构成的集合)
(2)对应关系(对应法则):
函数概念的核心是变量y与变量x之间的对应法则。通俗的来讲,1个x只能对应1个y,而1个y可以对应多个x。
(3)值域:函数的值域是函数值的集合。(函数的定义域和对应关系确定了,函数的值域也确定了)
3、函数的表示方法:
(1)解析法:数学表达式来表示两个变量之间的对应关系的方法;
(2)列表法:自变量取值(有限)与函数值之间的关系;
(3)图像法:自变量取值范围与函数值取值范围。
例题1:如图所示中,哪一幅图象不是函数?

答:第四副,因为根据函数的定义可知,前三副图象满足“一个x对应一个y”,而第四副则不是。
例题2:下列函数中,哪两个函数为同一函数?
①y=|x|(0<x<1)、②y=x-1、③y=x(0<x<1)、④y=x+1
答:①和③,因为这两个函数的定义域都是“0<x<1”,值域都是“0<y<1”,且对应法则相同。
1、增函数:一般地,设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量的值x₁、x₂,当x₁>x₂时,都有f(x₁)>f(x₂);
2、减函数:一般地,设函数f(x)的定义域为I,如果对于定义域I内某个区间D上的任意两个自变量的值x₁、x₂,当x₁>x₂时,都有f(x₁)<f(x₂)。
1、偶函数:一般地,设函数f(x)的定义域为I,如果对于定义域I内的任意一个x,都有f(x)=f(-x);
2、奇函数:一般地,设函数f(x)的定义域为I,如果对于定义域I内的任意一个x,都有f(-x)=-f(x)。
(下面举例几个常见函数)
1、定义:最高次数是二次且最高次数项是系数不为0的函数。一般表达式为y=ax²+bx+c(a、b、c为常数且a≠0)。
2、性质:
①图象:对称轴平行于(包括重合)y轴的抛物线。
②常见的形式:(1)一般式:y=ax²+bx+c(a≠0);(2)顶点式:y=a(x-h)²+k(a≠0);(3)交点式:y=a(x-m)(x-n)(a≠0)
③交点公式、对称轴和顶点:
交点公式:(-b±√(b^2-4ac))/2a;
对称轴:直线x=(-b)/2a;
顶点坐标:((-b)/2a, (4ac-b^2)/4a)。
对称轴与顶点之间的关系:设对称轴为直线x=t,顶点坐标为(t,c-t^2)。
两交点之间的距离:|x₁-x₂|=√(b²-4ac)/(|a|)。(证明可查看初中数学——二次函数)
④二次函数中,a的大小决定开口方向及开口大小。
(1)当a>0时,二次函数开口向上;当a<0时,二次函数开口向下。(2)当a越大时,二次函数开口越小;当a越小时,二次函数开口越大。(可以尝试画一下图象)
⑤二次函数中,b和a共同决定对称轴的位置。(1)当b=0时,对称轴为y轴;(2)当b/a>0(a、b同号)时,对称轴在y轴左侧;(3)当b/a<0(a、b异号)时,对称轴在y轴右侧。
⑥c(c≠0)为二次函数与y轴的唯一交点的纵坐标,(1)当c=0时,二次函数过原点;(2)当c>0时,二次函数与y轴交于正半轴;(3)当c<0时,二次函数与y轴交于负半轴。
1、根式:
(1)n次方根的概念:一般地,如果b^n=a(n>1,n∈N+),那么b叫做a的n次方根。记作:
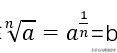
(2)n次方根的性质:
①当n是奇数时,正数的n次方根是正数;负数的n次方根是负数。
②当n是偶数时,正数的n次方根有两个;负数没有n次方根。
③0的任何次方根都是0。
(3)根式的概念:式子
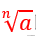
叫做根式,n(n>1,n∈N+)叫做根指数,a叫做被开方数。
(4)根式的性质:
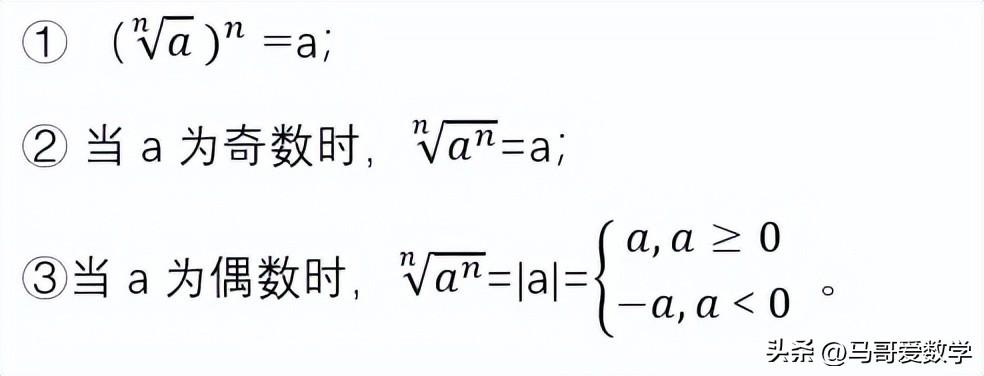
2、分数指数幂:

3、幂函数:
(1)概念:一般地,形如y=x^α(α∈R)为幂函数,底数x是自变量,底数的系数为1,指数a为常数。
(2)性质:
①函数的图象一定会经过第一象限内,一定不会出现在第四象限内。
证明如下:若x>0时,则y>0(包含α=0)
②函数的图象最多只能同时出现在两个象限内。
(第一象限或第一象限、第二象限或第一象限、第三象限)(根据α的大小而定)
③所有幂函数在(0,+∞)都有意义,且函数图象都经过(1,1)。
(此时未去除“α=0”的情况 )
④当α>0时,幂函数的图象经过原点,且在【0,+∞)上是增函数;当α>1时,幂函数的图象下凸;当0<α<1时,幂函数的图象上凸;当α<0时,幂函数在定义域内为减函数。
(当α<0时,自变量x作分母;当0<α<1时,函数图象靠近y轴;当α>1时,函数图象靠近x轴)
4、指数函数:
(1)概念:一般地,形如y=a^x(a>0且a≠1)称为指数函数,函数的定义域为R,值域为(0,+∞)。
(2)性质:
①函数图象必经过(0,1);
②当0<a<1时,函数在R上为单调减函数:
(1)如果x>0,那么0<y<1;
(2)如果x<0,那么y>1。
④当a>1时,函数在R上为单调增函数:
(1)如果x>0,那么y>1;
(2)如果x<0,那么0<y<1。
1、对数的概念:
一般地,如果a^b=N(a>0且a≠1)那么b叫做以a为底N的对数,记作
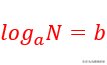
其中a叫做底数,N叫做真数
即:

2、常用对数和自然对数:
常用对数:以10为底的对数,可以简记为lgN。
自然对数:以无理数e=2.71828……为底的对数,可以简记为lnN。
3、对数基本性质:

4、对数公式:(a>0且a≠1,M>0,N>0)

对数的加、减、乘、除法以及换底公式
5、对数函数:
(1)概念:一般地,形如

的函数,对数函数的定义域为(0,+∞),值域为(-∞,+∞)。
(2)性质:
①函数图象必经过(1,0)
②当a>1时,函数在(0,+∞)上为增函数:
(1)如果x>1,那么y>0;
(2)如果0<x<1,那么y<0。
③当0<a<1时,函数在(0,+∞)上为减函数:
(1)如果x>1,那么y<0;
(2)如果0<x<1,那么y>0。

宇宙间藏满了无数的函数……