

一、温馨提示:
阿基米德原理用公式表示为F=G排,使用公式时应注意以下几点;
(1)原理中所说的“浸在液体里的物体“包含两种状态:
一是物体的全部都浸人液体里,称为“物体浸没在液体里”。
二是物体的一部分浸人液体里,另一部分露在液面以上。
(2)G排是指被物体排开的液体所受的重力,即物体排开多少牛的液体,物体所受到的浮力就是多少牛。
(3)G排=p液gV排中,p液表示液体的密度,V排表示被物体排开的液体的体积。当物体浸没在液体里时,V排=V物;当物体只有一部分浸入液体时,V排<V物。
如果物体三分之一的浸入液体中
则V排=(1/3)V物
(4)由F浮=G排=p液gV排可知,
浮力的大小只液体的密度和物体排开的液体的体积两个因素有关,
而跟物体本身的材料、体积、密度、形状、深度,液体的多少等因素无关。
(5)阿基米德原理也适用于气体。
即F浮=G排=p气gV排
此时p气是气体的密度,
V排是表示被物体排开的气体的体积。
(6)物体浸在液体(或气体)中的体积就是物体排开液体(或气体)的体积。
二、典型题目解析:
例题1、弹簧测力计下挂一个物体,弹簧测力计的示数为G,把该物体浸没在甲液体中,弹簧测力计的示数为G/3;
把该物体浸没在乙液体中,弹簧测力计的示数为G/4,则甲乙两种液体的密度之比是( )
解析:
求浮力大小的两种方法:
1、弹簧测力计法求浮力大小的方法F浮=G—F示
2、阿基米德原理
F浮=G排=m排g=p液gV排
注意:浸没时V排=V物
由题意得:
物体浸没在甲液体中时,
G—G/3=p甲gV物 (1)
物体浸没在乙液体中时
G—G/4=p乙gV物 (2)
(1)(2)两式联立解得
p甲:p乙=8:9
例题2、将金属块挂在弹簧测力计下端,先后浸没在水和酒精中,金属块静止时弹簧测力计的示数如图1中甲、乙所示,已知酒精的密度是0.8g/cm3,下列关于金属块的几个物理量,计算正确的是:
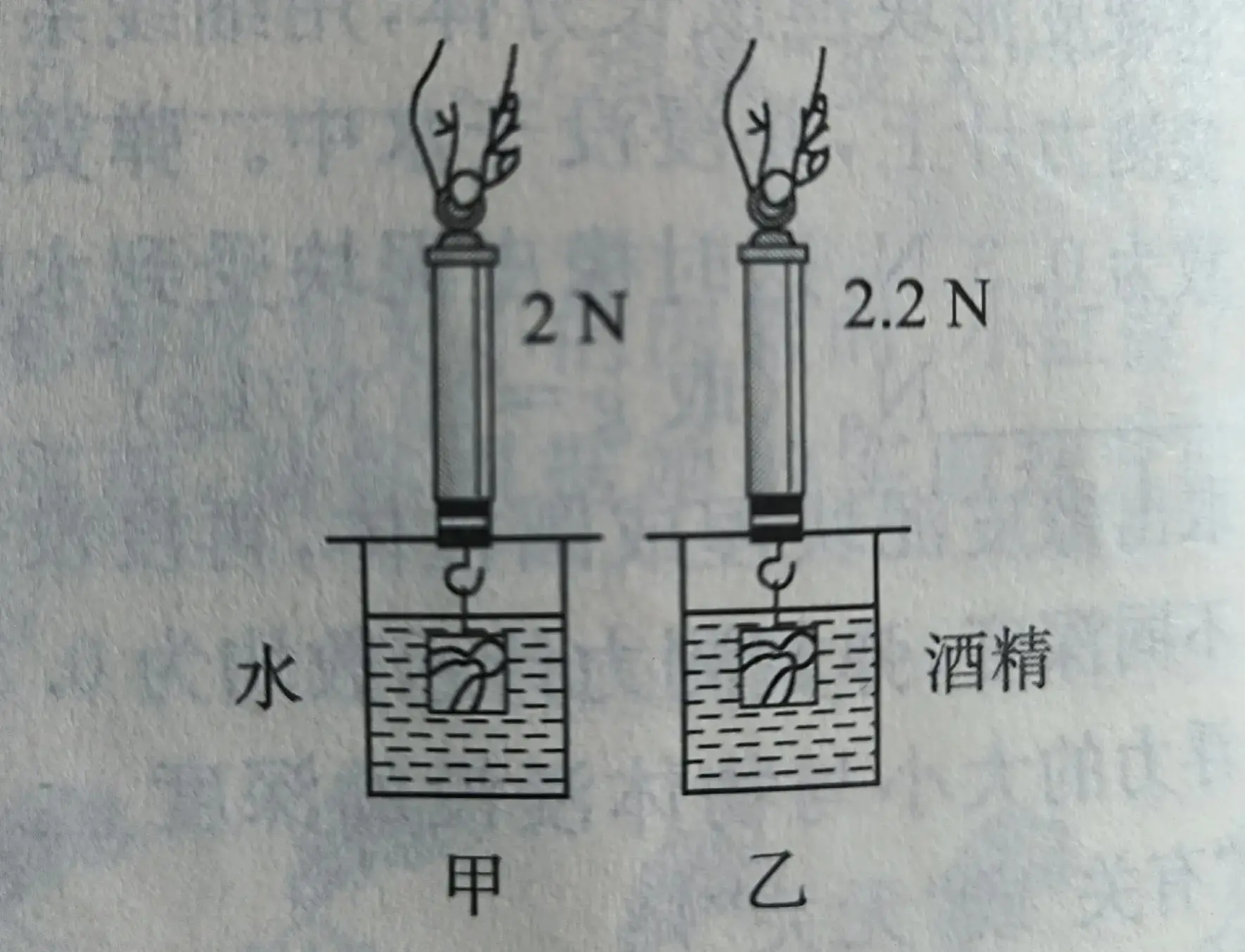
图1
A.在水中受到的浮力为2N
B.质量为3kg
C.体积为10cm3
D.密度为3g/cm3
解析:
假设物体重G,
由于是浸没,所以
V排水=V排酒=V物
由题意得
G—2N=p水gV物
G—2.2N=p酒gV物
上两式联立解得G=3N
物体质量m=G/g=3N/10N/kg=0 3kg
V物=100cm³=10-4m³
物体密度p物=m物/V物
=0.3kg/10-4m³
=3x10³kg/m³=3g/cm³
故正确答案选D
3.如图2甲所示,一弹簧测力计下挂一圆柱体,将圆柱体从水面上方某一高度处匀速下降,然后将圆柱体逐渐浸入水中。整个过程中弹簧测力计的示数F与圆柱体下降高度h的关系如图2乙所示。
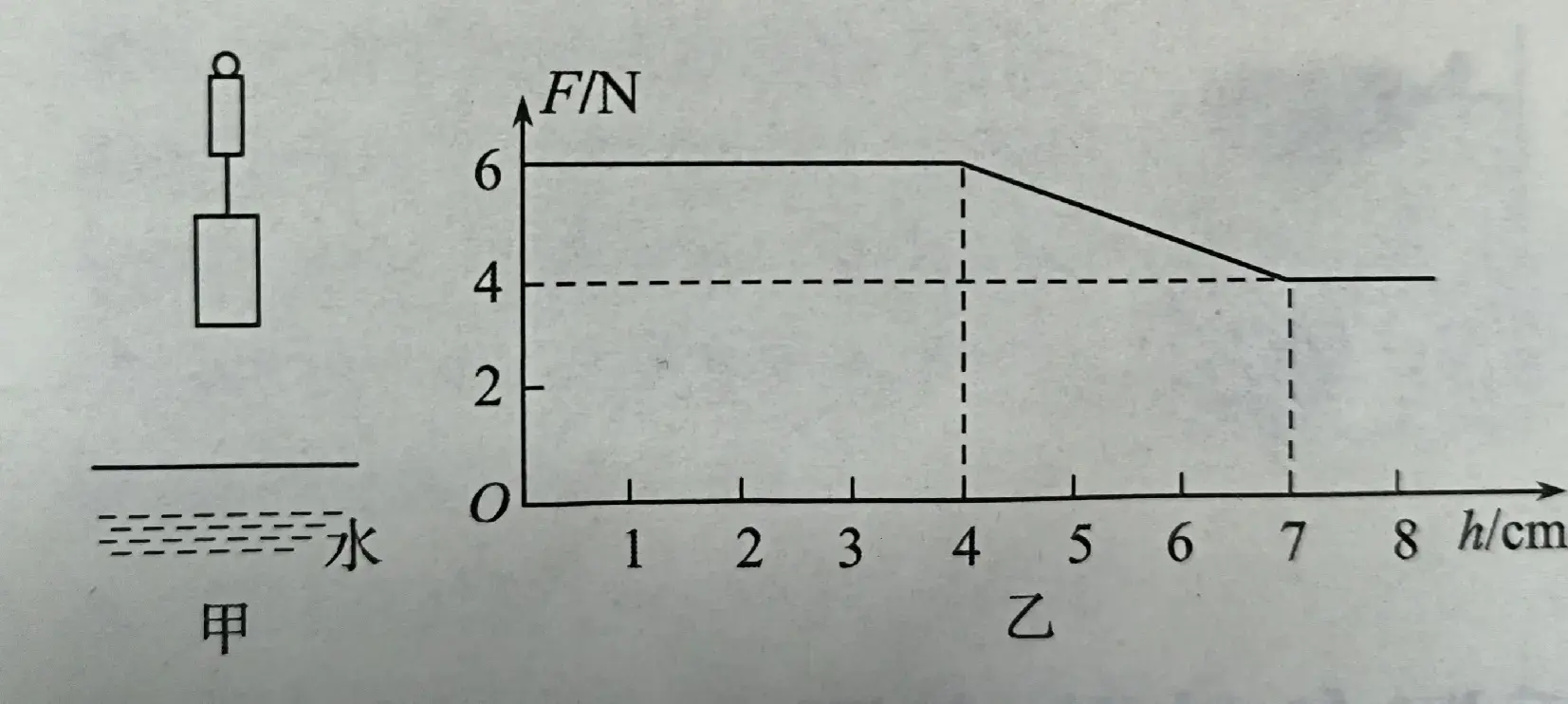
图2
求:
(1)圆柱体的重力。
(2)当圆柱体刚好全部浸没时,下表面受到水的压强。
(3)圆柱体的密度。
解析:(1)由甲图知,圆柱体的重力G=6N
(2)由图乙可知 ,下降高度4cm到7cm之间的过程,是圆柱体从底部开始接触水面,到圆柱体完全浸没在水中的过程,
由此可知圆柱体的高度是7cm—4cm=3cm,也就是圆柱体刚好全部浸没时,下表面所在的深度:
h=7cm—4cm=3cm=0.03m
根据计算液体压强的公式,
P=pgh
=1000kg/m³
x10N/kg
x0.03m=300pa
(3)分析乙图得,当圆柱体下降的高度是7cm时,它刚好全部浸没(V排=V物)在水中,此时弹簧测力计的示数为4N。
则圆柱体浸没时所受浮力的大小:(弹簧测力计法)
F浮=G—F示=6N—4N=2N
根据阿基米德原理
F浮=G排=p水gV排
=p水gV物
则圆柱体的体积
V物=F浮/p水g
=2N/1.0X10³kg/m³
x10N/kg)
=2x10-4m³
G=mg
圆柱体质量m=G/g
=6N/(10N/kg)=0.6kg
则圆柱体的密度:
p=m/v
=0.6kg/(2x10-4m³)
=3X10³kg/m³
跟踪练习:
如图3甲所示,一个质量为270g的铝块悬挂在弹簧测力计的挂钩上,铝块的下表面刚好接触某未知液体的液面。将铝块缓慢浸入液体,弹簧测力计的示数随浸人深度的变化如图3乙所示。
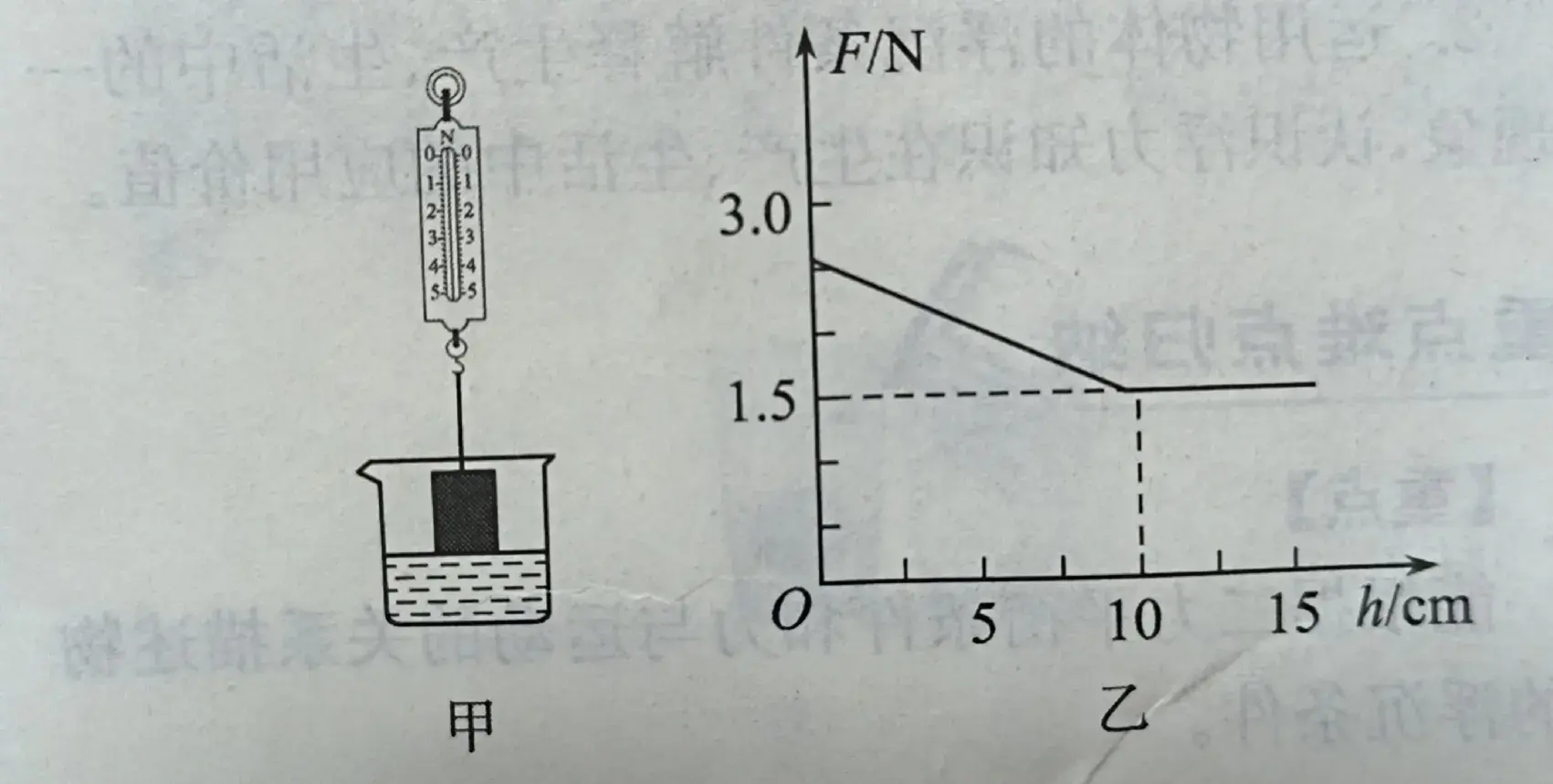
图3
则铝块浸没时所受的浮力为( )N,液体的密度为( )kg/m3。(取g=10N/kg,p铝=2.7X10³ kg/m³)。
答案:1.2,1200。
温馨提示:
(1)知道铝块的质量,可以根据G=mg求出它的重G。
分析图乙铝块浸没时,弹簧测力计的示数为:
F示=1.5N
然后根据弹簧测力计法,铝块浸没时所受到的浮力:
F浮=G—F示
=2.7N—1.5N=1.2N
(2)浸没时
V排=V铝=m铝/p铝
=270g/(2.7g/cm³)
=100cm³=10-4m³
根据阿基米德原理
F浮=G排=p液gV排
=p液gV铝
p液=F浮/gV铝
=1.2N/(10N/kgx10-4m³)
=1.2X10³ kg/m³