


A.若母线在坐标面上,且轴是坐标轴,那么可以直接套用公式:
f(y,z)=0&x=0绕z轴旋转→z不变,把原方程里面的y改为±sqrt(y^2+x^2)→f(±sqrt(y^2+x^2),z)=0.
例如:

要算三重积分,先要得到曲面方程
题目中的曲面,可以直接利用公式得到z^2+y^2=2x
B.增加一点难度,若母线不在坐标面上(母线任意),还是绕着z轴旋转,那么可以先读懂如下原理:
绕z轴旋转,那么转出来的点z坐标都不变,旋转的点和原始的点到z轴的距离一样。
再把原理变为方法:
把原母线变为参数方程,则原母线上的点记为x_t,y_t,z_t,旋转面上的点记为x,y,z,绕z轴旋转→z不变→z=z_t,距离一样→x^2+y^2= x_t ^2+y_t ^2,最后消去参数t,便可得x,y,z满足的方程。
例如一道2013年数学一的题:

因为母线不在坐标面上,所以没法用简单的方法A,要计算曲面的方程,只能利用方法B
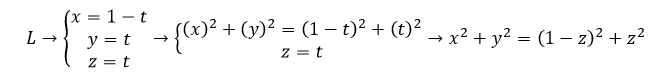
C.终极方法,当旋转轴不是坐标轴时,只能用专业的旋转面构造方法了,其实以上的方法都是专业方法的特殊情况,方法AB的原理都是方法C,一般来说考研,学会方法AB就行了,方法C有点太专业(太难了)。
原理:曲面上任一点满足的方程就是曲面方程。点P(x,y,z)要在旋转面上需要满足,P由母线上的点旋转而得(到轴的距离一样,和轴垂直),将这些要求写成参数方程组后消去参数即可。之前的方法AB,都是由这个推导出来的。例如
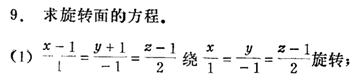
因为轴不是z轴,没法用方法AB,只能从方法C入手
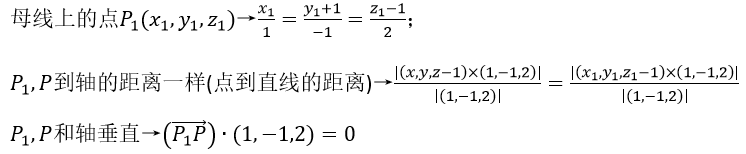
接下来把上面的方程组消去参数x_1,y_1,z_1(四个方程消去三个参数,可得一个方程),就是P(x,y,z)满足的旋转面方程。