

分式这一章整体来说难度不大,但是有些知识点却很容易出错,我们在解题时要特别注意。本章突出了类比思想,从分数有意义的条件、为零的条件、正负数的条件、约分、通分、性质、运算法则等,类比引出分式有意义的条件、约分通分等知识点,对比学习收获会更大。那么,在分式的基本概念中,有哪些内容需要我们注意呢?这些知识点不要再错了。

一般地,如果A、B(B不等于零)表示两个整式,且B中含有字母,那么式子A / B 就叫做分式,其中A称为分子,B称为分母。因此,判定一个代数式是不是分式,关键是看分母中有没有字母,并且看的是形式,不是最终化简的结果。

观察分母中有没有字母,①中分母为2,是数字不是未知数,因此不是分式;
②中分母为x,刚学习时有些同学可能会比较迷惑,这个可以化简为2x,应该为整式不是分式,其实不是的,分式看的是形式,不是最终化简的结果,因此②是分式;
③也要注意,分母中是π,π是无理数,不是未知数,因此不是分式;
④中分母为R,虽然不是x,也是未知数,因此是分式;
⑤中分母为未知数,是分式。

分式有意义的条件可以参考分数有意义的条件,即当分母B≠0时,分式有意义。

要使分式①有意义,则分母x-2≠0,即x≠2时,分式有意义;
要使分式②有意义,则分母x^2+1≠0,由x^2≥0可知,则x^2+1≥1恒成立,即分母不可能等于0,那么x可取全体实数;
要使分式③有意义,则分母x^2-9≠0,即x≠±3,分式有意义。
分式要为0,那么需要满足的条件除了分子等于0以外,不要忘记分母还不能为0,如果仅仅满足分子为0,此时分母还等于0,那么分式仍然没有意义。因此,分式为0的条件有两个:(1)A=0;(2)B≠0.
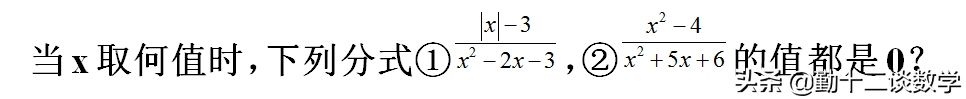
要使得分式①的值为0,那么需要满足分子| x | -3=0,可得x=±3,但是当x=3时,分母为0,因此需要舍去,答案为-3.
要使得分式②的值为0,那么需要分子x^2-4=0,可得x=±2,但是当x=-2时,分母为0,因此需要舍去,答案为2.

当分子、分母同号时,分式的值为正,即A>0、B>0或A<0、B<0时,分式的值为正;当分子、分母异号时,分式的值为负,即A>0、B<0或A<0、B>0时,分式的值为负。

分式的值为正数,因此需要分两种情况讨论,分子、分母要么同为正,要么同为负,即第一种情况:x-1>0,x+2>0,解得:x>1;第二种情况:x-1<0,x+2<0,解得:x<-2;综上所述:x>1或x<-2.

分式的基本概念,这些知识点不要再错了。