

奇偶性,其实核心就2句话4个核心点:
偶函数:y轴对称,f(x)=f(-x);
奇函数:原点对称,f(x)=-f(-x).
看偶函数:
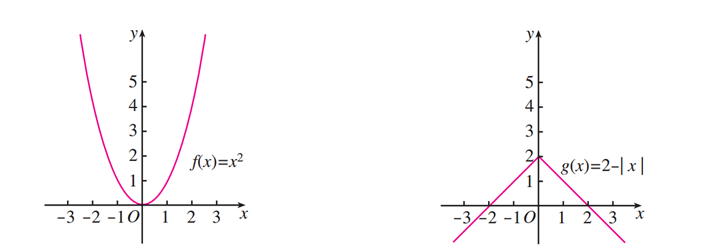
我们会发现,当x取相反数时,函数值是相同的,就是关于y轴对称,就有f(x)=f(-x)。

再来看奇函数:
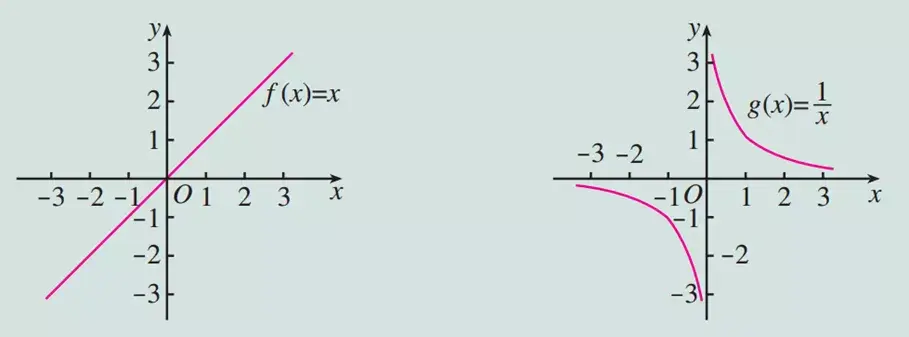
我们会发现,当x取相反数时,函数值是相反的,就是关于远点对称,就有f(x)=-f(-x)。即

令x=0,则有f(0)=-f(0),即f(0)=0;
所以对于奇函数,若在x=0处有定义,一定有f(0)=0;
注意:判断一个函数的奇偶性时,先去看定义域对不对称,比如[-3,2],对于x=-3来说,x=3都不在定义域,肯定不是奇偶函数!
最后,强调一下,核心就是2句话4个核心点:
偶函数:y轴对称,f(x)=f(-x);
奇函数:原点对称,f(x)=-f(-x).